Any equation that can be rearranged to the form $ax^2+bx+c=0$ can be solved with the quadratic formula. The formula will lead to one of:

two, real, distinct solutions
one, real, repeated solution
no real solutions

As we have seen on factored form to graph, the solutions to $ax^2+bx+c=0$ are the $x$ -intercepts of the parabola $y=ax^2+bx+c$ .

This parabola has two, real, distinct $x$ -intercepts:

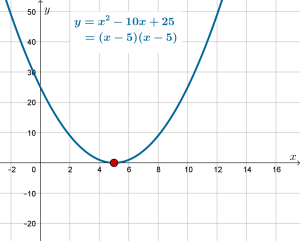
This parabola has one, real, repeated $x$ -intercept:

This parabola has no real $x$ -intercepts. (We can define complex solutions but these are not included in this course).

Solution by factoring

If the solutions of the equation $ax^2+bx+c=0$ are whole numbers, or even reasonably simple fractions, the most efficient method to solve the equation is by factoring.

For example:

To find the $x$ -intercepts we solve:

$\begin{align*}x^2-15x+36&=0\\[10 pt](x-3)(x-12)&=0\\[10 pt]x=3 \quad \text{or} \quad x&=12\end{align}$

If, however, the parabola cuts the $x$ -axis at points other than integer values it is not easy to factor. For example:

The solutions $x=1.42$ and $10.58$ are found using the quadratic formula.

The quadratic formula

If $ax^2+bx+c=0$ then $x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

How it works

Solve

$x^2-12x+15=0$

This equation is already in the form $ax^2+bx+c=0$ , so it is easy to identify the parameters $a, b$ and $c$ .

$a=1, \quad b=-12 \quad c = 15$

Substitute these values to the formula we have:

$\begin{align*}x&=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\\[10 pt]&=\dfrac{-(-12)\pm\sqrt{(-12)^2-4(1)(15)}}{2(1)}\\[10 pt]&=\dfrac{12 \pm \sqrt{84}}{2}\end{align}$

We can now type these two values (the plus and the minus) into the calculator:

$x_1=\dfrac{12-\sqrt{84}}{2}=1.42, \quad \quad x_2=\dfrac{12+\sqrt{84}}{2}=10.58$

Video link

Practice

Kuta Software worksheet to practice applying the quadratic formula.

Find the roots of the parabolas in this applet. Use the quadratic formula, or perhaps factor if the expression factors easily. Round answers correct to 2 decimal places.

Applet link