The first ten positive multiples of 3 are
{3,6,9,12,15,18,21,24,27,30}
Multiples can be positive whole numbers, negative whole numbers or zero. We often use a horizontal number line to visualize multiples. On this number line, we begin from zero:
The multiples of a number are the answers when you multiply your number by another number. Or, in other words, the answers you get when you repeatedly add the same number starting from zero.
In this activity, we divide the circumference of a circle into12 equal parts. Below is the applet that you can use for each of the diagrams, or you can print it out from the 12 point circle pdf to use a ruler, pencil, colouring pencils – have a blast!
Getting started:
Reset between diagrams, or take a new printed circle for each item:
- Starting with 0, join the multiples of 2 in sequence
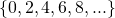 ;
; - Starting with 0, join the multiples of 3 in sequence
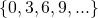 ;
; - Starting with 0, join the multiples of 4 in sequence
 ;
;
Factors: 1, 2, 3, 4, and 6 are all factors of 12. They can be written in pairs so that the product is 12:
![]()
![]()
![]()
In other words, the factors of 12 are all the whole numbers that divide 12 to give an answer that is a whole number.
![]() and
and ![]()
![]() and
and ![]()
![]() and
and ![]()
A ‘factor of a number’ is a whole number that divides the number with no remainder.
Next Up
Reset between each diagram, or use a different printed circle:
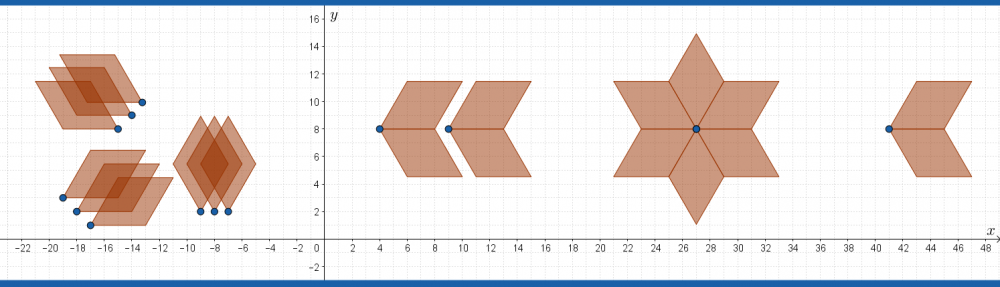
- Start at zero and go up in two’s as before. Then start at one and go up in twos, until you get back to where you started. All the points should now be used!
- Start at zero and go up in three’s. Then start at one and go up in three’s. Then start at two and go up in three’s. All the points should now be used!
- Start at zero and go up in four’s. Then at start at one; then start at two; then at three. It takes four loops to visit every point when going up in fours!
More Focus Required:
- Start at zero and go up in 5’s. Keep going around and around until you get back to the first point. You should use all the points, and the star should be symmetrical!
- How many times do you pass ‘zero’ when you go up in 5’s?
- Suppose you label each point with numbers and keep labelling up to 60 – for example, the 0 point is also the 12 point and the 24 point etc. What will all the numbers beside the number ‘3’ point be? What about the number ‘7’ point?
- How many lines of symmetry does your star diagram have? What about rotational symmetry?
- Now try going up in 7’s – what’s the same, and what’s different?
Other circles
Suppose you draw a 9 or a 15 or a 24 point circle. Applets for 24, 15, 9 point circles here.
- Use the factors of the number of points to draw various polygons.
- Which polygons can be drawn without any edges intersecting other edges?
- What happens when you use a number that has no common factors with the number of points?
- What happens when you use a number that is not itself a factor, but shares a common factor with the number of points?
Going beyond!
Open Ended:
On your own geogebra file, draw a circle using the formula ![]() . Decide how many points you want on your circle. Plot points using sines and cosines, for example, to mark the ‘zero’ type into the input bar: A=(cos(90°),sin(90°)). Copy and paste for speed! How to video here.
. Decide how many points you want on your circle. Plot points using sines and cosines, for example, to mark the ‘zero’ type into the input bar: A=(cos(90°),sin(90°)). Copy and paste for speed! How to video here.
Extension to graph theory: The form made when joining multiples of 5 up to 60 (a closed loop) is considered isometric to a dodecagon in graph theory. Find out more about that here! (Page 15)
Extension to modular arithmetic: The numbers 13 and 49 are said to be congruent to each other, in the class of the remainders of 12 (we say ![]() ). Find out more here!
). Find out more here!